Xác định lực căng của cáp đo lực căng dây cáp trong cầu dây văng hay cáp dự ứng lực
Ngày đăng:10:10 09/12/2021
Lượt xem: 5.115
Cỡ chữ


Xác định lực căng của cáp, đo lực căng dây cáp trong cầu dây văng hay cáp dự ứng lực (DƯL) ngoài trong giai đoạn khai thác là rất cần thiết cho việc kiểm tra và đánh giá thường xuyên cầu treo dây văng.
Phương pháp phổ biến nhất hiện nay để xác định lực căng trong cáp bằng thực nghiệm là phương pháp dựa trên kết quả đo dao động xác định tần số dao động riêng thứ nhất của cáp. Tuy nhiên, phương pháp này có thể không chính xác trong trường hợp các thông số độ võng và độ cứng chống uốn của cáp lớn.
Trong nghiên cứu này, đo lực căng dây cáp dựa trên các phương trình đặc trưng dao động riêng cáp có xét đến độ võng và độ cứng chống uốn với nhiều dạng dao động khác nhau.
Bằng cách xem xét các giả định đơn giản hóa các thông số độ cứng để tìm ra lời giải của phương trình thu được và xác định lực căng của cáp dựa trên các dạng dao động khác nhau.
Phương pháp này sử dụng kết quả đo dao động để tính toán lực căng trong cáp dựa trên tần số dao động theo các dạng dao động khác nhau của cáp. Kết quả nghiên cứu được áp dụng đánh giá lực căng trong cáp của cầu Phú Mỹ dựa trên số liệu đo dao động thực tế của 4 cáp cầu dây văng Phú Mỹ, TP. Hồ Chí Minh.
Giới thiệu chung đo lực căng dây cáp
Việc đo lực căng dây cáp là một vấn đề quan trọng để kiểm soát trạng thái làm việc theo thời gian của các cáp dây văng trong cầu dây văng và cầu khẩu độ lớn sử dụng cáp DƯL ngoài.
Trong các nghiên cứu trước đó, cách tiếp cận bán thực nghiệm hoặc mô hình số học đã được sử dụng để đánh giá lực căng trong cáp dựa trên một mô hình đơn giản lý tưởng hóa. Kovacs (1982) lần đầu tiên xác định đươc sự hiện hữu của một kích thước tối ưu cho cáp DƯL ngang được thêm vào bộ giảm chấn dạng nhớt.
Sau đó, Yoneda - Maeda (1989), Uno và cộng sự (1991) đã tiến hành nghiên cứu số học về kích thước bộ giảm chấn tối ưu và đã chỉ ra rằng khả năng giảm chấn tối đa có thể đạt được tỷ lệ thuận với khoảng cách giữa bộ giảm chấn và neo cáp và độc lập với số mode dao động.
Đáng chú ý là kết quả nghiên cứu của Pacheco và các cộng sự (1993) về hướng đơn giản hóa các bước thiết kế giảm chấn dạng nhớt cho cáp văng. Gần đây, hiệu ứng uốn ở các phương thức giảm chấn của cáp căng với bộ giảm chấn đã được nghiên cứu phân tích bởi nhiều tác giả trong đó có kết quả nghiên cứu của (Hoang và Fujino 2007).
Tại Việt Nam, ngày càng nhiều các dự án cơ sở hạ tầng mới ở cấp quốc gia được lên kế hoạch và ngày càng có nhiều cầu được xây dựng. Cho đến nay, đã có nhiều công trình cầu treo được xây dựng và đưa vào khai thác có chiều dài nhịp chính trên 300m như: Cầu treo dây võng Thuận Phước (nhịp chính 450m), cầu dây văng Mỹ Thuận (nhịp chính 350m); Cần Thơ (nhịp chính 550m); Rạch Miễu (nhịp chính 270m); Bãi Cháy (nhịp chính 435m) và gần đây nhất là cầu Phú Mỹ tại TP.Hồ Chí Minh (nhịp chính 380m, Hình 2.3a, 2.3b), cầu Nhật Tân (nhịp chính 300m).
Ngoại trừ cầu Mỹ Thuận là cầu treo dây văng có nhịp lớn đầu tiên tại Việt Nam thì các cầu treo dây văng khác đều được lắp đặt hệ thống quan trắc sức khỏe (hệ thống SHM) như cầu Rạch Miễu, cầu Cần Thơ, cầu Nhật Tân...
Tuy nhiên, ngay cả với các cầu đã lắp đặt hệ thống quan trắc thì chỉ một số nhỏ các cáp được lắp đặt sensor đo kiểm tra lực căng bằng Loadcell hoặc đầu đo gia tốc. Do vậy, vẫn cần các giải pháp thực nghiệm hoặc bán thực nghiệm để xác định và kiểm soát lực căng của cáp trong giai đoạn vận hành, khai thác cầu. Trong nghiên cứu này, nhóm nghiên cứu đề xuất phương pháp đánh giá lực căng của cáp bằng phương pháp bằng đồ thị, nhằm đánh giá một cách rõ ràng lực căng trong cáp so với các phương pháp sử dụng trước đây và có xét đến các thông số như độ võng, độ cứng chống uốn của cáp, cũng như ảnh hưởng của bộ giảm chấn trong cáp.
Cơ sở lý thuyết đo lực căng dây cáp
Phương trình dao động cơ bản của cáp
Phân tích mô hình dao động của một cáp nghiêng dưới tác dụng đo lực căng dây cáp của lực căng T như thể hiện trong Hình 2.1. Hệ tọa độ khảo sát theo trục x dọc theo trục cáp và trục y theo hướng vuông góc. Thông số tính toán của cáp: Khối lượng trên đơn vị chiều dài: m, chiều dài dây cáp L, độ cứng chống uốn EI và góc nghiêng θ so với phương nằm ngang (0 ≤ θ < π/2). Phương trình dao động của cáp trong mặt phẳng v(x, t) (theo phương y) được Fujino và Hoàng 2008 [1] , Hiroshi Zui và cộng sự 1996 [2] đề xuất như sau:
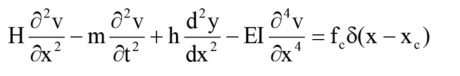
Trong đó: H = Th/cosθ - Lực căng dây; T h - Thành phần lực theo phương ngang của lực căng cáp; δ(x-x c } - Hàm Dirac xác định hiệu quả của lực giảm chấn f c (t) ở vị trí x = x c ; v(x, t) - Dao động theo phương ngang (hướng trục y).
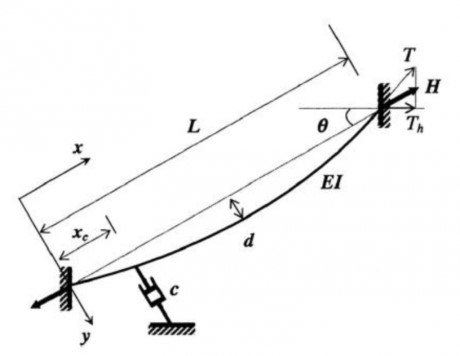
Hình 2.1: Mô hình phân tích dao động của 1 cáp nghiêng đo lực căng dây cáp
Công thức (1) đã giả thiết rằng lực căng T là đủ lớn để độ võng của cáp có thể được biểu diễn chính xác bằng đường parabola (Irvine 1981) [3] .
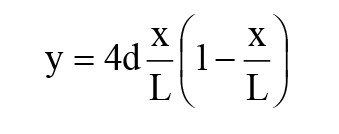
Với d - Độ võng tại vị trí giữa của cáp, d = mgL 2 cosθ/(8H), g - Gia tốc trọng trường. Trong công thức (1), h(t) là lực căng biến đổi theo vị trí, lấy được từ khả năng tương thích giữa tính đàn hồi và hình học của phần tử cáp (Irvine và Caughey 1974) [4] .
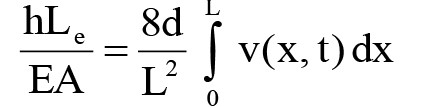
Trong đó: EA - Độ cứng dọc trục của cáp và .L e = L[1+8](d/L) 2 công thức (1) tương ứng với các trường hợp chung nhất của cáp khi xét đến cả độ võng và độ cứng chống uốn đều được đưa vào tính toán. Đối với dao động tự do của cáp, hàm chuyển vị, lực cản của giảm chấn và lực căng biến đổi theo vị trí được viết lại như sau:
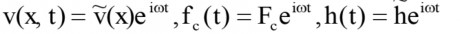
Trong đó: i 2 =-1, ω - Tần số dao động riêng,
- Hàm dạng dao động riêng của cáp. Phương trình đã được nghiên cứu bởi tác giả đầu tiên đánh giá hiệu ứng giảm chấn của dây cáp văng với bộ giảm chấn (Fujino và Hoàng 2008). Hai thông số quan trọng là (i) thông số độ võng λ 2 xác định bởi Irvine và Caughey (1974):
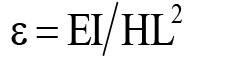
(ii) - Độ cứng chống uốn e (Hoang and Fujino 2007) [5] :
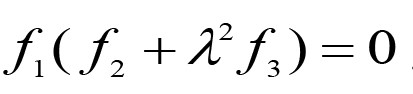
Xem xét sự dao động tự do của dây cáp với tần số tự nhiên ω. Từ đó, biểu thị các tham số thứ nguyên ví dụ số bước sóng , phương trình đặc trưng sau đây cho bcó thể được suy ra (Fujino và Hoang 2008) khi lực giảm chấn = 0:
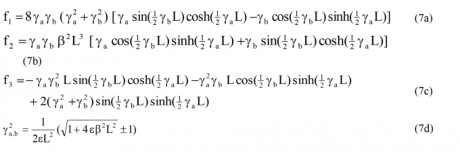
Cần lưu ý rằng, trong trường hợp dạng dao động không đối xứng thì độ võng sẽ không làm tăng thêm lực căng cho cáp đo lực căng dây cáp. Kết quả là tồn tại các nghiệm khác nhau của phương trình (7) cho các dạng dao động gần đối xứng và bất đối xứng của cáp có giảm chấn. Với dạng dao động bất đối xứng (mode dao đông thứ n = 2, 4,…), số bước sóng có thể xác định bằng cách cân bằng giá trị f 1 đầu tiên ở công thức (7) đến giá trị 0:
Với các dạng dao động đối xứng (mode dao động thứ n = 1, 3,…), tính các phần trong dấu ngoặc bằng 0.
Phương trình (7) và kết hợp với (8 & 9) là phương trình siêu việt, có thể giải được với số tham số bsử dụng phương pháp số lặp, như Newton-Raphson, bắt đầu bằng một giá trị thích hợp. Ta thấy phương trình này hàm chứa một loạt các vấn đề với một trong hai tham số: Tham số độ võng λ 2 hoặc tham số độ cứng chống uốn eđược kèm theo riêng biệt. Ví dụ, số bước sóng của một dây cáp uốn căng (λ 2 = 0) được xác định bằng cách cân bằng kết quả của phép tính f 1 × f 2 về 0, mà có kết quả tương tự như phương trình cáp đặc trưng đề xuất bởi Zui và cộng sự (1996). Khi λ 2 ≠ 0, trong giới hạn của độ cứng chống uốn e 0, sau khi sắp xếp lại biểu thức trong ngoặc và đưa nó về 0, ta thu được phương trình số bước sóng cho cáp võng (không uốn) được thành lập bởi Irvine và Caughey (1974).